The following is the full Q&A for the interview from Phys.org.
1. Could you explain to our readers how your recent paper published in Nature Physics came about, what main ideas or theories it was based on, and what its main objectives were?
This work started from my intellectual pursuit of trying to understand how machines can perceive, manipulate, and process quantum systems and quantum information.
During my undergraduate, my research centers around statistical machine learning and deep learning. A central basis for the current machine learning era is the ability to utilize highly parallelized hardware, such as graphical processing units (GPU) or tensor processing units (TPU). It is natural to wonder how an even more powerful learning machine capable of harnessing quantum-mechanical processes could emerge in the far future. This has been my aspiration when I started my Ph.D. at Caltech.
In order to approach such an ambitious future on firm ground, the first step is to understand how machines can perceive, manipulate, and process quantum systems and quantum information. The standard technique known as quantum state tomography learns the entire description of a quantum system, which requires an exponential number of measurements, memory, and time. This characteristic makes machines unable to perceive quantum systems with more than tens of qubits. Recently, neural network approaches have been proposed, demonstrating surprisingly strong empirical performance in several cases, but lacks a clear understanding of when it would work or fail.
To build a rigorous foundation for how machines can perceive quantum systems, we combined my previous knowledge about statistical learning theory with Richard Kueng and John Preskill’s expertise on a beautiful mathematical theory known as unitary t-design. Statistical learning theory is the theory that underlies how the machine could learn an approximate model about how the world behaves. Unitary t-design is a mathematical theory that underlies how quantum information scrambles, which is central to understand quantum many-body chaos, in particular, quantum black holes. Together, it results in a rigorous and efficient procedure for a classical machine to construct an approximate classical description of a quantum many-body system. The classical description allows accurate prediction of many properties of the quantum system from only performing a minimal amount of quantum measurements.
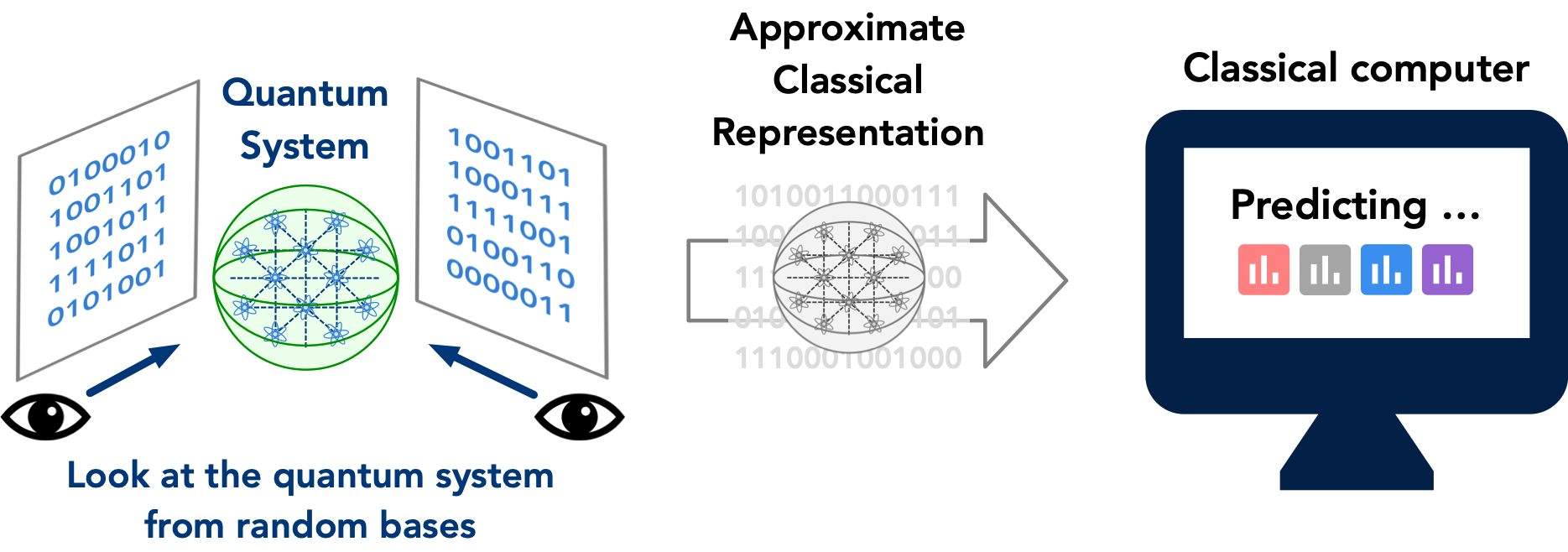
2. In relatively simple terms, could you explain how the method for constructing an approximate classical description of a quantum state works, outlining its key advantages/unique characteristics?
To construct an approximate classical description of the quantum state, we perform a randomized measurement procedure given as follows. We sample a few random quantum evolutions that would be applied to the unknown quantum many-body system. These random quantum evolutions are typically chaotic and would scramble the quantum information stored in the quantum system. This random quantum evolution is where the connection to the mathematical theory on unitary t-design used in the study of quantum many-body chaos, such as quantum black holes, comes about. Then we look at each of the randomly scrambled quantum systems with a measurement apparatus, which would result in a wave function collapse that turns the quantum system into a classical system. The data characterizing the random quantum evolutions and the resulting classical systems after the measurement are combined to form an approximate classical description of the quantum system.
Intuitively, one could think of this procedure as follows. We have an exponentially-high dimensional object, the quantum many-body system, that is very hard to grasp by a classical machine. We perform several random projections of this extremely high dimension object to a much lower dimensional space through the use of random/chaotic quantum evolution. The set of random projections provides a rough picture of how this exponentially high dimensional object looks like. And the classical representation allows us to predict various properties of the quantum many-body system.
Building on statistical learning theory and the theory of quantum information scrambling, we prove a surprising statement showing that this procedure could accurately predict M properties of the quantum system from only log(M) measurements. For example, by measuring the quantum system for a number of times, we can predict an exponential number of properties for the quantum system.
On the other hand, the traditional understanding is that when we want to measure M properties, we have to measure the quantum system M times. This is because after we measure one property of the quantum system, the quantum system would collapse and become classical. After the quantum system has turned classical, we can not measure other properties with the resulting classical system. Our approach avoids this by performing randomly generated measurements and infer the desired property by combining these measurement data.
This provides a rigorous understanding of some of the surprisingly strong performance seen in recent machine learning approaches. Furthermore, building on this theoretical foundation, the proposed method can be orders of magnitude faster than existing machine learning approaches and provide a more accurate prediction for existing highly specialized quantum information techniques in measuring various properties of the quantum many-body system.
3. What do you feel are the most meaningful achievements of your study, and what insight do these bring to the Physics field?
Our study rigorously shows that there is much more information hidden in the data obtained from quantum measurements than we originally expected. By suitably combining these data, we can infer this hidden information and gain significantly more knowledge about the quantum system. This implies the importance of data science techniques for the development of quantum technology. Furthermore, we show that to fully utilize the power of machine learning, an understanding of the strange behavior intrinsic to quantum physics is decisive. The direct application of standard machine learning techniques could be partially successful. But the full potential only becomes evident when we combine the mathematics underlying machine learning and quantum physics in an organic fashion.
4. What are your plans for future research?
Given a rigorous ground for perceiving quantum systems with classical machines, my personal plan is to take the next step towards creating a learning machine capable of manipulating and harnessing quantum-mechanical processes. In particular, we want to provide a solid understanding of how machines could learn to solve quantum many-body problems, such as classifying quantum phases of matter or finding quantum many-body ground states. The ability to construct efficient classical representations of quantum systems opens a gateway for classical machine learning to tackle these challenging quantum many-body problems from a rigorous footing. However, perceiving is not enough for solving these quantum problems. The machines would also have to learn to simulate certain computations to succeed. This would be a further synthesis between the underlying mathematics of machine learning and quantum physics.
At the same time, we are also working on refining and developing new tools for inferring hidden information from the data collected by quantum experimentalists. The physical limitation in the actual systems provides interesting challenges for developing more advanced techniques. This would further allow experimentalists to see what they originally could not and help advance the current state of quantum technology.
Publication:
Predicting many properties of a quantum system from very few measurements (Nature Physics 2020).
https://www.nature.com/articles/s41567-020-0932-7